The metric system, you know, is an international decimal system of weights and measures. It came about in France way back in 1795, and it's now used officially in so many places around the globe. This system is built on uniformity and simplicity, a concept developed by the Paris Academy of Sciences. It has main units for length, like the meter, and for mass, like the kilogram. For instance, the length of a typical guitar is about one meter, which gives you a good idea of its size. This system uses metres, centimetres, litres, and other similar units for measuring things, which is pretty straightforward.

When we talk about "metric," it usually refers to this system of measurement. While the word "metric" can also mean a descriptive statistic or an indicator in other areas, here we are talking about how we measure things. The metric conversion staircase helps us see how these measurements relate to each other. It shows how one unit can be changed into another, making conversions much clearer. This guide will walk you through this visual aid, making those changes from one unit to another feel much more natural, and perhaps, even a little fun.

Table of Contents

• Understanding the Metric System Basics
• What is the Metric Conversion Staircase?
  • The Steps of the Staircase
  • Base Units and Their Place
• How to Use the Staircase for Conversions
  • Moving Down the Staircase: Multiplying
  • Moving Up the Staircase: Dividing
• Practical Examples for Length, Mass, and Volume
  • Length Conversions
  • Mass Conversions
  • Volume Conversions
• Common Questions About Metric Conversions
• Tips for Remembering the Staircase

Understanding the Metric System Basics

The metric system is a way of measuring things that is, you know, very logical. It's based on powers of ten, which makes it easy to change between different unit sizes. This is a big reason why it revolutionized global measurement with its uniformity. For instance, a meter is ten decimeters, a decimeter is ten centimeters, and so on. This decimal basis is what makes the "staircase" method work so well, too it's almost like counting by tens.

The system has three main units for different types of measurement. The meter is for length, like how long something is. The kilogram is for mass, which is how much "stuff" is in something. And the liter is for volume, which measures how much space something takes up. These are the foundational elements, you know, the building blocks of the entire system. It is a system of measuring that is very widely accepted.

Beyond these main units, there are prefixes that tell us how big or small a unit is compared to the base. For example, "kilo" means a thousand, so a kilometer is a thousand meters. "Centi" means one-hundredth, so a centimeter is one-hundredth of a meter. These prefixes are key to the metric conversion staircase, as a matter of fact, they are the names of the steps.

What is the Metric Conversion Staircase?

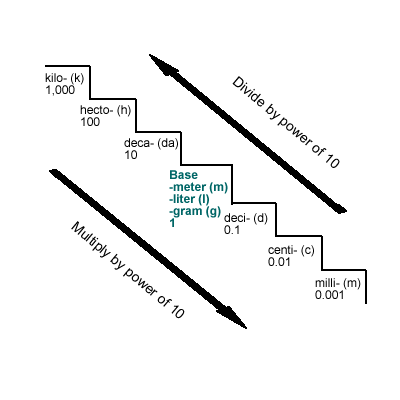
The metric conversion staircase is a visual aid that helps people change one metric unit into another. It is a way to remember the order of metric prefixes and how to move between them. Think of it like a set of stairs where each step represents a different power of ten. When you go up or down these stairs, you are essentially multiplying or dividing by ten, which is pretty neat. This simple picture, you know, really helps clear things up.

This method is especially helpful for students and anyone who needs to do quick conversions without a calculator. It provides a simple rule to follow, making it less likely to make mistakes. It helps you see the relationship between units, like how many millimeters are in a meter, or how many kilograms are in a gram. It's a practical tool for learning more about metric systems with ease, actually.

The Steps of the Staircase

Imagine a staircase with seven steps. Each step has a specific name, which is a metric prefix. From the top step to the bottom, these prefixes typically go like this:

• Kilo (k)
• Hecto (h)
• Deka (da)
• Base Unit (meter, gram, liter)
• Deci (d)
• Centi (c)
• Milli (m)

These prefixes, you know, help define the size of the unit. Kilo is the largest shown here, and milli is the smallest. Each step down means the unit is getting smaller, and each step up means it's getting larger. This setup, you know, gives us a clear path for conversions.

Base Units and Their Place

Right in the middle of our staircase is the "base unit." This is where the core measurement lives. For length, the base unit is the meter. For mass, it's the gram. And for volume, it's the liter. So, if you're working with length, your staircase might look like kilometer, hectometer, dekameter, meter, decimeter, centimeter, millimeter. This is where your starting point usually is, you know, the main measurement.

The base unit is important because all other units on the staircase are defined in relation to it. For example, a centimeter is one-hundredth of a meter, and a kilometer is one thousand meters. This central position makes it easy to visualize how far you need to move to get to your desired unit. It's the anchor point, as a matter of fact, for all your conversions.

How to Use the Staircase for Conversions

Using the metric conversion staircase is actually quite simple. You start by figuring out where your current unit is on the staircase and where your target unit is. Then, you count the number of steps you need to move to get from one to the other. This number of steps tells you how many places to move your decimal point. It's a very visual way to approach these calculations, you know, almost like a little dance for numbers.

The direction you move on the staircase determines whether you multiply or divide. If you are going from a larger unit to a smaller unit, you will multiply. If you are going from a smaller unit to a larger unit, you will divide. Each step represents a factor of ten, so you just move the decimal point one place for each step. This method helps to avoid the need for complex formulas or calculators for basic conversions, which is pretty handy.

Moving Down the Staircase: Multiplying

When you move down the staircase, you are going from a larger unit to a smaller unit. For example, if you go from meters to centimeters, you are moving down two steps. Each step down means you multiply by ten, or simply move the decimal point one place to the right. So, for two steps, you move the decimal point two places to the right. This makes sense because you need more of the smaller units to equal one of the larger units, obviously.

Let's say you have 5 meters and want to know how many centimeters that is. You start at "meter" and go down two steps to "centimeter." So, you move the decimal point in 5.0 two places to the right, making it 500. Therefore, 5 meters is 500 centimeters. This rule applies consistently across all base units, you know, for length, mass, and volume. It's a very consistent system, in fact.

This process is like breaking a big piece into many smaller pieces. For instance, if you have one large cookie and want to share it in tiny crumbs, you'll have a lot of crumbs. Similarly, one large unit converts into many smaller units. This method helps you visualize that increase in quantity, which is pretty useful, you know, for understanding the change.

Moving Up the Staircase: Dividing

When you move up the staircase, you are going from a smaller unit to a larger unit. For instance, if you want to change millimeters to meters, you are moving up three steps. Each step up means you divide by ten, or just move the decimal point one place to the left. So, for three steps, you move the decimal point three places to the left. This is because you need fewer of the larger units to equal many smaller units, you know, it's just how it works.

Consider if you have 2500 milliliters and you want to know how many liters that is. You start at "milliliter" and go up three steps to "liter." So, you move the decimal point in 2500.0 three places to the left, making it 2.5. Thus, 2500 milliliters is 2.5 liters. This makes conversions from tiny measurements to bigger ones much clearer, as a matter of fact, it's quite straightforward.

This process is like grouping many small items into fewer, larger groups. For example, if you have many tiny beads and you put them into bags, you'll have fewer bags than beads. Likewise, many small units convert into fewer larger units. The staircase helps you visualize this decrease in quantity, which is really quite helpful, you know, for grasp the concept.

Practical Examples for Length, Mass, and Volume

The beauty of the metric conversion staircase is that it works for all types of metric measurements: length, mass, and volume. The steps and the rules for moving the decimal point remain the same, regardless of the base unit. This uniformity is a core principle of the metric system itself, which is based on the meter for length and the kilogram for mass, as adopted in 1795. It means once you learn the staircase, you can apply it broadly, which is very convenient.

Let's look at some examples for each type of measurement. These examples will show you how to apply the "move the decimal" rule in real situations. It's a very practical way to learn, you know, by doing. These examples help you see the system in action, which is quite useful.

Length Conversions

Length measurements use the meter as their base unit. The staircase for length would be: kilometer, hectometer, dekameter, meter, decimeter, centimeter, millimeter. You can think of distances or sizes, you know, like the length of a room or a piece of string. This setup helps you figure out how many smaller units are in a larger one, or vice versa.

Example 1: Convert 3.5 kilometers to meters.
Start at kilometer. Move down three steps to meter (kilo -> hecto -> deka -> meter).
Move the decimal point three places to the right.
3.5 becomes 3500.
So, 3.5 kilometers is 3500 meters. This is a very common conversion, you know, for things like road signs.

Example 2: Convert 800 millimeters to meters.
Start at millimeter. Move up three steps to meter (milli -> centi -> deci -> meter).
Move the decimal point three places to the left.
800.0 becomes 0.800.
So, 800 millimeters is 0.8 meters. This is useful for small measurements, you know, like the width of a pencil.

Example 3: Convert 15 centimeters to decimeters.
Start at centimeter. Move up one step to decimeter (centi -> deci).
Move the decimal point one place to the left.
15.0 becomes 1.5.
So, 15 centimeters is 1.5 decimeters. This shows how you can move between adjacent steps, too it's almost effortless.

Mass Conversions

Mass measurements use the gram as their base unit. The staircase for mass would be: kilogram, hectogram, dekagram, gram, decigram, centigram, milligram. This is about how much "stuff" something contains, like the weight of an apple or a bag of sugar. It helps you change between different scales of mass, you know, from very light to very heavy.

Example 1: Convert 2 kilograms to grams.
Start at kilogram. Move down three steps to gram (kilo -> hecto -> deka -> gram).
Move the decimal point three places to the right.
2.0 becomes 2000.
So, 2 kilograms is 2000 grams. This is a common conversion for cooking or buying groceries, you know, it's quite practical.

Example 2: Convert 500 milligrams to grams.
Start at milligram. Move up three steps to gram (milli -> centi -> deci -> gram).
Move the decimal point three places to the left.
500.0 becomes 0.500.
So, 500 milligrams is 0.5 grams. This is useful for very small amounts, you know, like in medicine.

Example 3: Convert 7.5 dekagrams to centigrams.
Start at dekagram. Move down two steps to centigram (deka -> gram -> centi).
Move the decimal point two places to the right.
7.5 becomes 750.
So, 7.5 dekagrams is 750 centigrams. This shows that you can start and end anywhere on the staircase, you know, it's quite flexible.

Volume Conversions

Volume measurements use the liter as their base unit. The staircase for volume would be: kiloliter, hectoliter, dekaliter, liter, deciliter, centiliter, milliliter. This measures how much space something occupies, like the amount of water in a bottle or the capacity of a swimming pool. It helps you change between different volumes, you know, from a tiny drop to a large tank.

Example 1: Convert 0.75 liters to milliliters.
Start at liter. Move down three steps to milliliter (liter -> deci -> centi -> milli).
Move the decimal point three places to the right.
0.75 becomes 750.
So, 0.75 liters is 750 milliliters. This is common for drinks or lab work, you know, it's very useful.

Example 2: Convert 1200 centiliters to liters.
Start at centiliter. Move up two steps to liter (centi -> deci -> liter).
Move the decimal point two places to the left.
1200.0 becomes 12.00.
So, 1200 centiliters is 12 liters. This helps when you have many smaller units and want to see the total in a larger unit, you know, it simplifies things.

Example 3: Convert 4.2 kiloliters to dekaliters.
Start at kiloliter. Move down two steps to dekaliter (kilo -> hecto -> deka).
Move the decimal point two places to the right.
4.2 becomes 420.
So, 4.2 kiloliters is 420 dekaliters. This shows the system's adaptability for larger volumes, you know, it's quite versatile.

Common Questions About Metric Conversions

People often have similar questions when they are getting to grips with metric conversions. It's a natural part of learning, you know, to wonder about the details. Here are some questions that often come up, along with simple answers using our staircase idea.

How many millimeters are in a meter?

To figure this out, you start at "meter" on the staircase and count the steps down to "millimeter." That's three steps down (meter to deci, deci to centi, centi to milli). Each step down means you move the decimal one place to the right. So, for three steps, you move the decimal three places to the right. This means there are 1000 millimeters in one meter. It's a very straightforward calculation, you know, once you see the steps.

What are the three main units of the metric system?

The metric system, you know, has three main units for different types of measurement. These are the meter for length, the gram for mass, and the liter for volume. These are the base units that sit in the middle of our conversion staircase. All other units are built around these three, you know, with prefixes telling us their size.

Why is the metric system easier than other systems?

The metric system is often seen as easier because it's a decimal system, meaning it's based on powers of ten. This makes conversions very simple, you know, just by moving the decimal point. Unlike other systems that might use different, less consistent conversion factors, the metric system's uniformity and simplicity, developed by the Paris Academy of Sciences, makes calculations much more direct. It's a very logical setup, you know, for measuring things.

Tips for Remembering the Staircase

Remembering the order of the prefixes on the metric conversion staircase can be a bit tricky at first. But there are some simple tricks that can help you keep them in mind. Using little memory aids, you know, can make a big difference. These tips are about making the order stick in your head.

One popular way to remember the order of prefixes is to use a mnemonic device. A common one is: "King Henry Died By Drinking Chocolate Milk." Each first letter of the words stands for a prefix:
K - Kilo
H - Hecto
D - Deka
B - Base (meter, gram, liter)
D - Deci
C - Centi
M - Milli
This little phrase, you know, helps you recall the order from largest to smallest. It's a very effective way to remember, as a matter of fact.

Another tip is to draw the staircase yourself a few times. The act of drawing and labeling each step can really help solidify the order in your mind. You can even draw little arrows pointing down for "multiply by 10" and arrows pointing up for "divide by 10." This visual practice, you know, reinforces the concept. It's a very hands-on approach to learning.

Practice, of course, makes perfect. The more you use the metric conversion staircase, the more natural it will become. Try converting different units every day, perhaps with a friend or family member. You can find many practice problems online or in textbooks. Consistent practice, you know, builds confidence and speed. Learn more about measurement systems on our site, and check out this page for more practice problems. This regular use will make the staircase a familiar and reliable tool for you, which is very helpful.

The metric system is a system of measuring that is very useful in many parts of life. Understanding how its units relate to each other through tools like the metric conversion staircase makes it much simpler. This method, you know, provides a clear, visual path for changing units. It takes away the guesswork and replaces it with a straightforward process. Keep practicing, and you'll find that metric conversions become a breeze, you know, very easy indeed. You can also look at other reputable science resources for more details on the history and applications of the metric system.